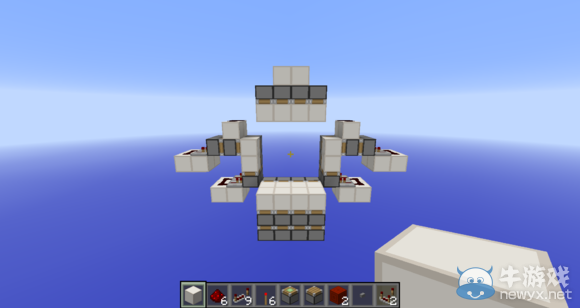
《我的世界》最小4x4高壓無痕內吸門建造方法介紹

時間：2015/01/07 17:47:12 編輯：Ocean

頁面導航：

第4頁：第4頁

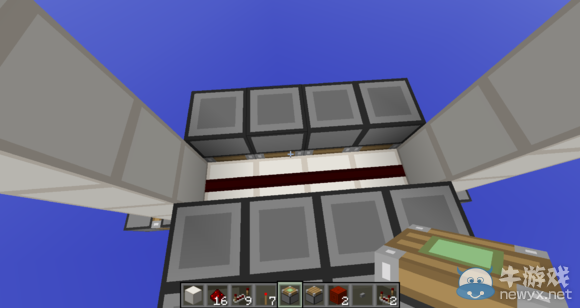
在關門的時序中有利用到一個活塞被斜角度激活的特性，除了這個地方，其他地方大家應該都可以理解。

右邊復制了一個和左邊一模一樣的側吸結構，這樣這個門的內吸部分的結構就都在圖中了。

接下來講的是這個門的無痕處理部分。（其實我在這個門的無痕處理部分上花了至少70%的時間...）←這句話無視，只是為了強調無痕處理部分的重要性。（話說這個門沒有無痕處理還稱得上是無痕內吸門么...）←廢話有點多233

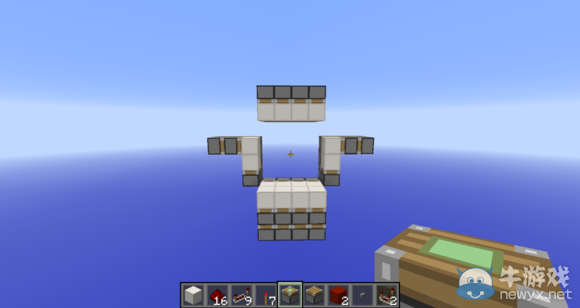
為了方便制作和講解，我暫時先把線路都打掉。

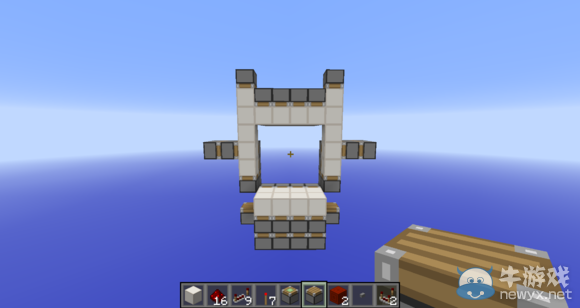
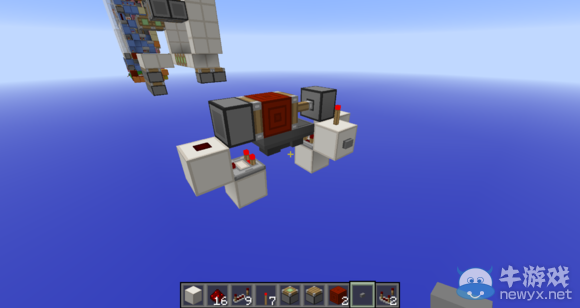
首先是最簡單的一個無痕處理，如圖，上方2個活塞各推一下，就實現了當前的無痕處理。關門時又需要有痕處理，那也十分簡單，下面另外放2個活塞，關門前各推一下就行了。

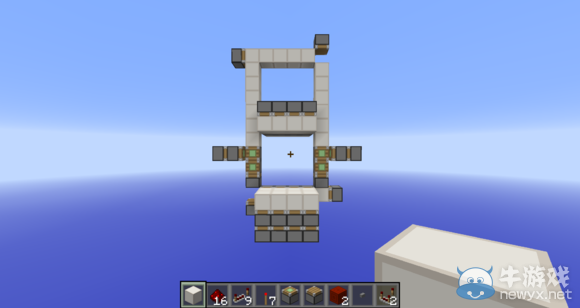
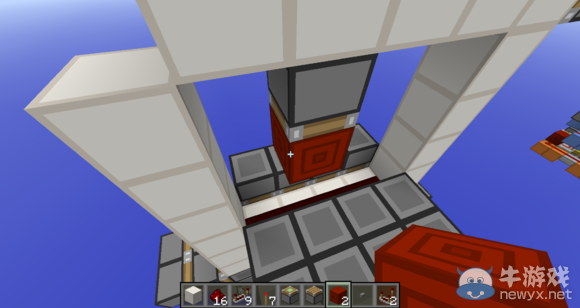
如圖，這是第二個無痕處理。（第一個無痕處理擋住了第二個無痕處理，為了方便講解我先把第一個無痕處理打掉了。）但為什么要把活塞輪擺的那么高呢？原因也很容易理解，如下圖。

可以看見這個輸入端已經無法從側邊通過給活塞輪的方塊充能來激活，因為會跟側吸部分有沖突，于是就要把活塞輪抬高，用下圖的方案。

就像這樣，就可以實現頂部正常開關門了。

第二個無痕處理，周期是28，也就是活塞輪驅動28下就是一個循環。

第三個無痕處理，周期是12，也就是活塞輪驅動12下就是一個循環。但這個活塞輪總共有24排方塊，為什么周期是12？原因很簡單，由于它本身用到了2處活塞放置處，且之間的間隔方塊列數相同，于是就可以把周期從原本的24降到12也就是除以2。

那么問題來了，如何做到每個活塞輪運轉的次數相同從而實現第一次輸入，輸出有痕處理，第二次輸入，輸出無痕處理，且可以反復使用呢？那么就要用到一個初中學到的知識，最小公倍數。

但是還有非常重要的一點。以第三個無痕處理為例，周期是12，其實這個無痕處理的輸出周期為6，已經可以實現開關門有痕和無痕處理，那么為了方便計算，我們就記下這個數字，6。同理，第二個無痕處理，周期是28，那么記下數字14。

為什么要記下這一系列的數字呢？就是為了方便計算整體無痕處理活塞輪周期。我們再以第三個無痕處理為例，當它運轉6次，可以實現開關門有痕和無痕處理。那么如果讓他運轉6*奇數次呢？這樣顯然也是可以的。同樣第二個無痕處理也可以讓他運轉14*奇數次。那么，我們只需要找一個特殊的最小公倍數。

從6和14中找一個最小公倍數，要保證最小公倍數分別除以6和14得到的結果為奇數。那么我們可以用死算（反正我是這么算出來的233）得到42，那么42就是這個門的無痕處理的整體活塞輪周期了！

這里給出一種活塞輪計時器的方案。

相關攻略

相關游戲